A principios de año apareció en Voz Pópuli un artículo titulado “En solo 320 segundos hackean a Bitcoin con el primer ataque cuántico de la historia”. El artículo generó un notable eco mediático y el propio medio finalmente modificó el titular por uno más prudente (aunque igualmente impreciso): “Un experto alerta de un posible intento de hackeo a Bitcoin con computación cuántica”.

El problema no es únicamente el alarmismo generado, sino que la premisa central del artículo es directamente falsa: no existe ningún ataque cuántico capaz de vulnerar Bitcoin usando un ordenador de 18 cúbits, ni en 320 segundos ni bajo ninguna otra condición realista.

Esta anécdota, sin embargo, sirve para repasar cómo funcionan distintos algoritmos de clave pública, explicar con claridad la criptografía que utiliza Bitcoin y entender qué requeriría realmente la computación cuántica para convertirse en una amenaza.

Además, conviene recordar que este tipo de narrativa no es algo aislado. Cada cierto tiempo reaparece la idea de que la computación cuántica está a punto de romper toda la seguridad basada en claves públicas, incluidas las infraestructuras de certificados que usamos a diario. Se suele presentar como uno de los primeros argumentos al hablar de ordenadores cuánticos, casi siempre sin matices. En este artículo veremos que estamos muy lejos de ese escenario. La computación cuántica no es magia ni un atajo inmediato para romper cifrados. Su estado actual está limitado por ruido, escalabilidad, fidelidad y la necesidad de corrección de errores masiva. Comprender estas limitaciones técnicas es clave para evaluar cualquier supuesto “ataque cuántico”.

RSA y el problema de la factorización

RSA, uno de los estándares clásicos de cifrado de clave pública, se basa en una idea muy sencilla: multiplicar dos números primos grandes es fácil, pero averiguar qué dos primos se usaron —es decir, factorizar el número resultante— es extremadamente difícil. Esa asimetría es la base de su seguridad y explica por qué un atacante debe invertir enormes recursos computacionales para romper una clave RSA convencional.

La construcción de RSA sigue siempre el mismo proceso: se escogen dos primos grandes (p y q), se calcula el producto n = p × q y, a partir de ahí, se derivan un exponente público e y un exponente privado d, donde d es el inverso modular de e respecto a (p−1)(q−1). El par (e, n) forma la clave pública, mientras que (d, n) constituye la clave privada. Sobre este mecanismo se construyen tanto el cifrado como la firma: el mensaje se eleva a una potencia módulo n, usando la clave pública para cifrar y la clave privada para firmar; el proceso inverso se realiza con la clave complementaria.

Por ejemplo, en un esquema RSA muy simplificado para propósitos didácticos, podríamos elegir p = 11 y q = 13, de modo que n = 11 × 13 = 143 y (p−1)(q−1) = 10 × 12 = 120. Para definir el exponente público seleccionamos un valor e que sea coprimo con 120, es decir, que no comparta factores con él. Probando valores pequeños vemos que 2, 3, 4, 5 y 6 no sirven, pero e = 7 sí cumple la condición (gcd(7,120) = 1). A partir de ahí calculamos el exponente privado d como el número que satisface e · d ≡ 1 (mod 120), lo que nos da d = 103. Así, la clave pública es (e, n) = (7, 143) y la clave privada es (d, n) = (103, 143). Si queremos cifrar un mensaje numérico pequeño, por ejemplo m = 9, el remitente calcula el cifrado c = m^e mod n = 9^7 mod 143; el receptor, con la clave privada, recupera el mensaje original computando m = c^d mod n. Aunque en la práctica se usan primos de cientos o miles de bits, la lógica matemática es exactamente la misma.

Las claves RSA modernas tienen normalmente 2048 bits, una longitud que garantiza que la factorización clásica resulte impracticable. Pero en 1994 Peter Shor demostró que un ordenador cuántico suficientemente grande podría factorizar estos números de forma eficiente mediante su algoritmo cuántico, lo que rompería RSA de forma directa.

El problema —y es la razón por la que RSA sigue siendo seguro hoy— es que ese “ordenador cuántico suficientemente grande” está muy lejos de la tecnología actual: sería necesario disponer de miles de cúbits lógicos, lo que se traduce en millones de cúbits físicos una vez añadida la corrección de errores cuánticos. No existe hoy ningún sistema que se acerque mínimamente a esa escala.

En entornos reales como TLS (y anteriormente SSL), RSA ha tenido tradicionalmente dos funciones: por un lado, autenticar al servidor mediante las firmas usadas en los certificados, algo que sigue siendo habitual; y por otro, servir como mecanismo de intercambio de claves, una función que hoy se ha abandonado porque no ofrece Forward Secrecy (es decir, que incluso si la clave privada del servidor se viera comprometida en el futuro, las sesiones cifradas del pasado seguirían siendo imposibles de descifrar).

En las versiones modernas del protocolo (TLS 1.3), el intercambio de claves se realiza mediante ECDHE (Elliptic Curve Diffie–Hellman Ephemeral), un mecanismo basado en curvas elípticas que genera claves efímeras para garantizar Forward Secrecy. Mientras tanto, RSA queda relegado a la autenticación del servidor o es sustituido directamente por firmas ECDSA (Elliptic Curve Digital Signature Algorithm), o incluso por algoritmos postcuánticos que comienzan a incorporarse progresivamente.

Para ver ejemplos reales, basta con comprobar los certificados de algunas webs muy conocidas. Amazon.com, por ejemplo, utiliza certificados basados en RSA de 2048 bits, algo que sigue siendo habitual en grandes plataformas por motivos de compatibilidad y estabilidad.

Por el contrario, Google.com es uno de los mejores ejemplos de un servicio que no utiliza RSA, sino certificados basados en ECDSA, normalmente con claves de curva elíptica secp256r1.

En la imagen siguiente puede apreciarse la diferencia entre ambos tipos de certificados al inspeccionar el campo Public Key Algorithm:

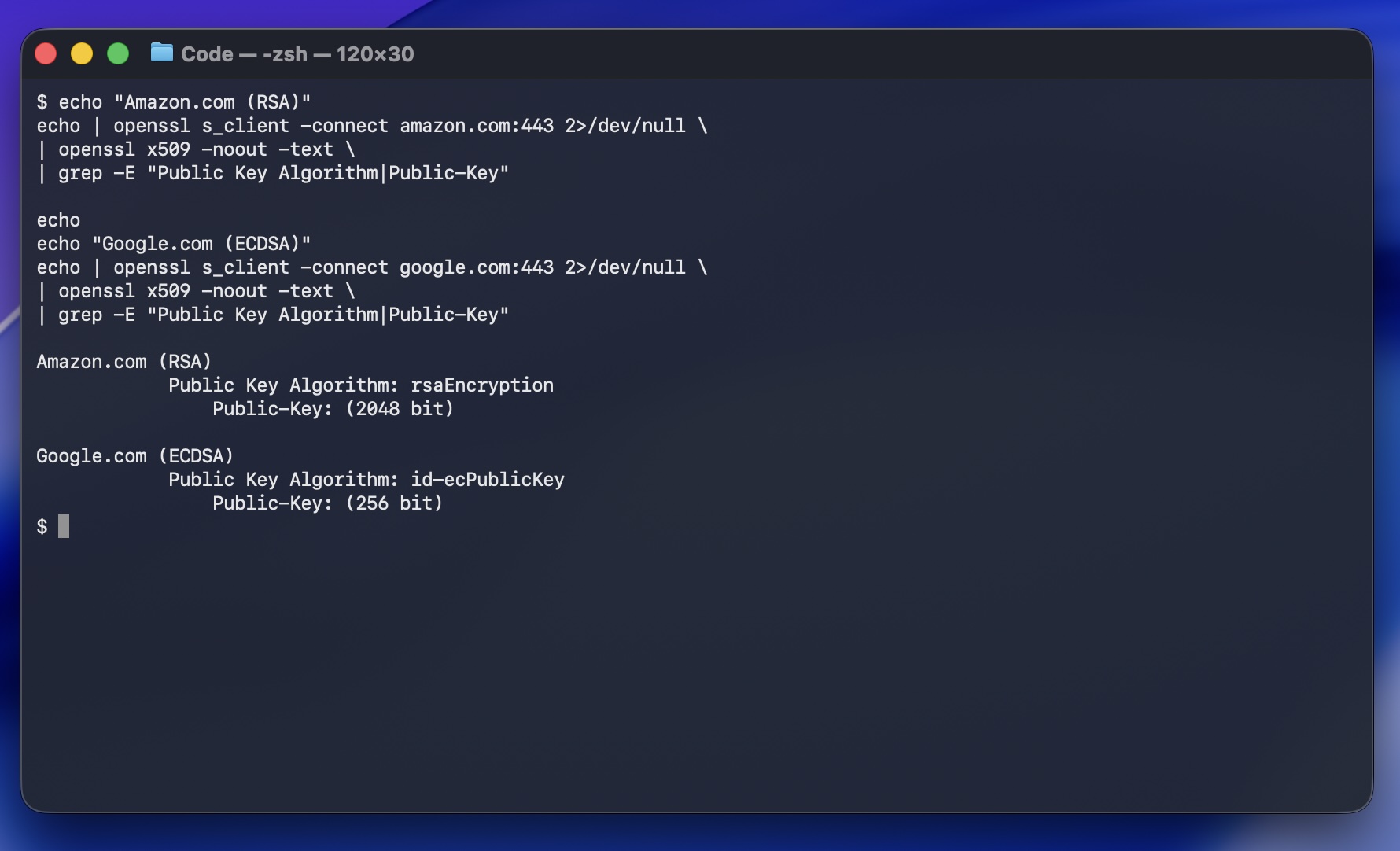
Ejemplo real: Amazon.com utiliza RSA de 2048 bits, mientras que Google.com utiliza ECDSA con claves de curva elíptica de 256 bits. La diferencia se aprecia comparando el campo “Public Key Algorithm” del certificado TLS.

RSA sigue siendo relevante, pero su futuro está condicionado por dos factores clave: la evolución real de la computación cuántica y la transición hacia algoritmos criptográficos postcuánticos, diseñados para resistir tanto ataques clásicos como ataques cuánticos. La solidez de RSA hoy no está en duda, pero a medio y largo plazo dependerá de cómo avance esta migración hacia estándares más robustos.

Criptografía de curvas elípticas

A diferencia de RSA, Bitcoin no se apoya en la factorización de números grandes, sino en la criptografía de curvas elípticas, concretamente en el esquema ECDSA utilizado sobre la curva secp256k1. Este enfoque permite ofrecer un nivel de seguridad muy alto con claves mucho más pequeñas.

ECDSA (Elliptic Curve Digital Signature Algorithm) es un algoritmo de firma digital que permite verificar que una transacción ha sido firmada por el propietario de una clave privada, sin revelar esa clave. La seguridad del sistema depende de la dificultad de resolver el ECDLP.

ECDLP (Elliptic Curve Discrete Logarithm Problem, o problema del logaritmo discreto en curvas elípticas) plantea lo siguiente: dado un punto P de la curva que resulta de multiplicar un punto base G por un número secreto k (es decir, P = k × G), es computacionalmente inviable calcular k. Multiplicar es fácil; invertir la operación es prácticamente imposible.

La curva usada por Bitcoin es muy simple en su definición matemática y se expresa mediante la ecuación:

y² = x³ + 7 (mod p)

donde p es un número primo de 256 bits. Aunque en la práctica se opera sobre un campo finito, esta representación continua ayuda a visualizar la forma de la curva:

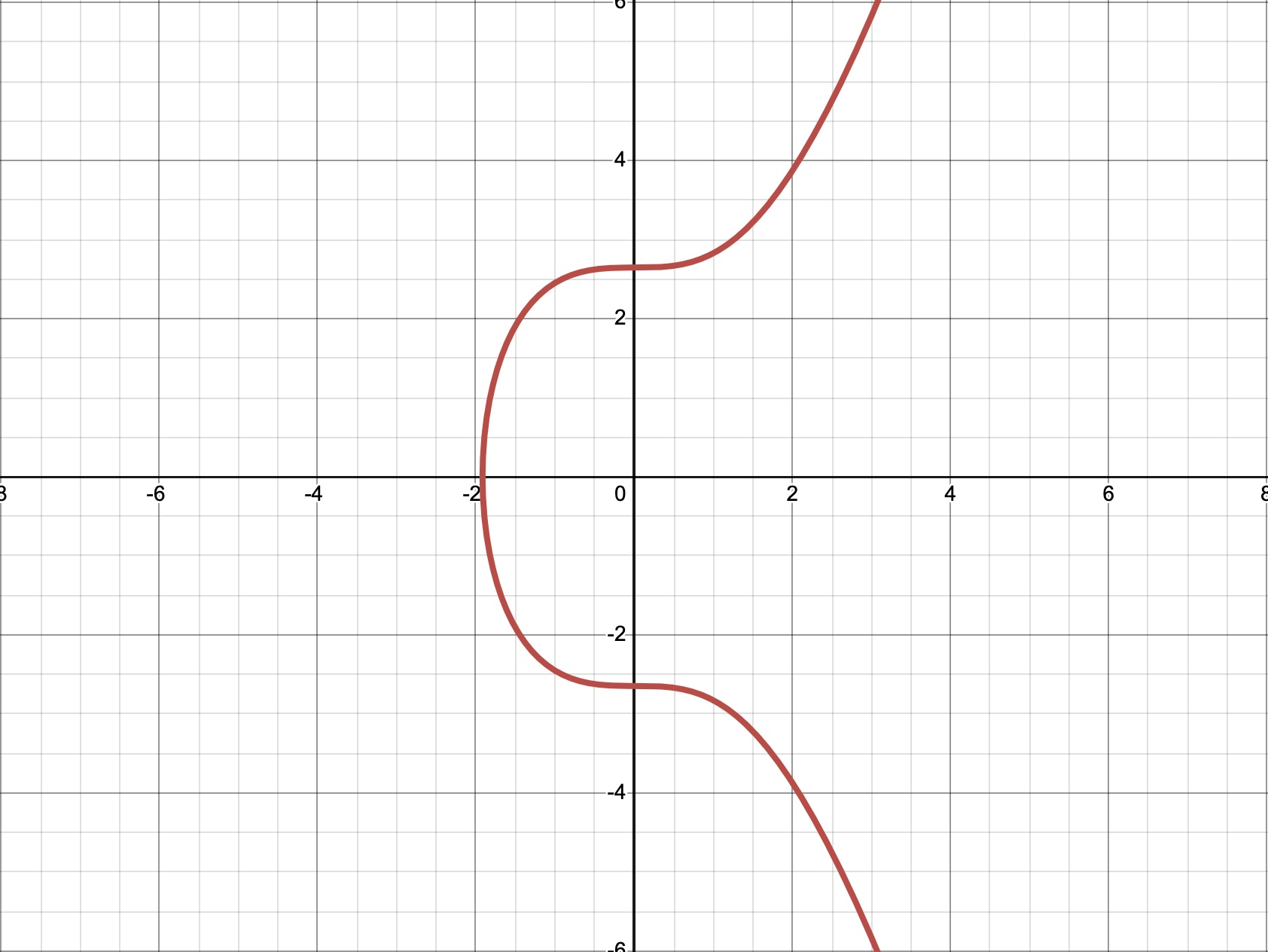Imagen 1. Representación gráfica de la curva elíptica y² = x³ + 7

Dentro de este sistema:

• La clave privada es un número entero de 256 bits.
• La clave pública es un punto de la curva, obtenido mediante la operación P = k × G, donde G es un punto base fijado por el estándar.
• A partir de la clave pública se genera la dirección de Bitcoin aplicando varias funciones hash.

La seguridad depende de que, aun conociendo G y P, nadie pueda recuperar el valor k. Esta dificultad es lo que hace que una clave de 256 bits en curvas elípticas ofrezca una seguridad equivalente a la de una clave RSA de más de 3000 bits.

Ejemplo sencillo de cómo funciona una curva elíptica

Para entender bien cómo funcionan las curvas elípticas en criptografía ayuda trabajar con un ejemplo pequeño y manejable. En lugar de usar la curva real de Bitcoin, que opera con números enormes de 256 bits, empleamos una curva diminuta definida sobre el campo finito módulo 17. Este tipo de curva no es segura, pero permite ver con claridad cómo se generan y manipulan claves sin necesidad de software especializado.

La curva que utilizamos es y² = x³ + 2 (mod 17). Elegimos este valor porque en módulos reducidos solo algunos parámetros producen curvas válidas y con suficientes puntos. El valor 2 genera una curva simple y funcional en este entorno. En Bitcoin se usa el parámetro 7 porque así lo fija el estándar secp256k1 y funciona correctamente en un módulo de 256 bits.

En un campo finito la curva no es continua. Es un conjunto discreto de puntos que cumplen la ecuación módulo 17. Con un módulo tan pequeño se pueden listar todos los puntos válidos de forma directa. Entre ellos está G = (0, 6) que empleamos como punto base. En sistemas reales como secp256k1 el punto base también está definido de antemano y garantiza las propiedades de seguridad necesarias.

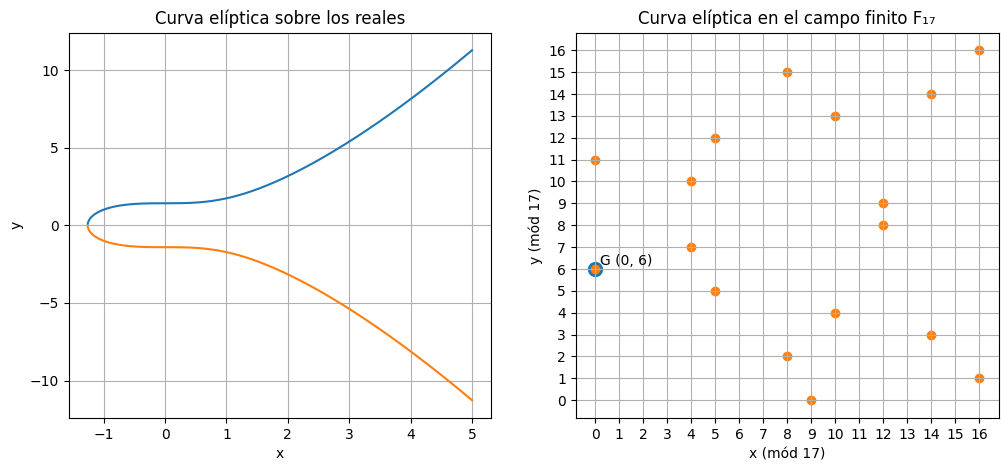
Imagen 2. Comparación entre la curva elíptica real y su versión discreta en el campo finito F₁₇

Clave privada y clave pública

Partimos de una clave privada pequeña, k = 7. En Bitcoin este valor sería un número aleatorio de 256 bits, pero aquí elegimos un número reducido para poder seguir el ejemplo sin esfuerzo.

La clave pública se obtiene mediante multiplicación escalar, expresada como P = k × G. En las curvas elípticas esta operación no es un producto convencional. Multiplicar un punto por un número significa sumarlo consigo mismo k veces aplicando las reglas específicas de la curva. En este caso:

P = 7 × G = G + G + G + G + G + G + G

Tras realizar cada una de estas sumas según las normas de la curva se obtiene P = (4, 12), que pasa a ser la clave pública correspondiente a la clave privada k.

Estas sumas no se comportan como operaciones en el plano habitual. La curva define un mecanismo geométrico propio. Cuando los puntos son distintos se toma la recta que los une, se identifica el tercer punto donde esa recta vuelve a cortar la curva y se refleja ese punto respecto al eje x para obtener el resultado. Cuando se suma un punto consigo mismo se utiliza la tangente en ese punto y se aplica el mismo procedimiento. Estas reglas se traducen en fórmulas exactas dentro del campo finito y permiten que la curva forme una estructura algebraica estable donde la multiplicación escalar tiene sentido y es eficiente de calcular.

Por qué es difícil invertir la operación

Intentar resolver P = k × G para encontrar k es el problema del logaritmo discreto en curvas elípticas. No existe ningún algoritmo eficiente que permita invertir esta operación en curvas modernas. La única estrategia general es la fuerza bruta. Examinar valores uno a uno hasta encontrar el correcto.

En el ejemplo esto sería posible porque el espacio de búsqueda es pequeño. En Bitcoin la clave privada tiene 256 bits y el total de valores posibles asciende a 2²⁵⁶, aproximadamente 1,15 × 10⁷⁷ opciones. Incluso un sistema capaz de probar mil millones de claves por segundo tardaría 10⁶⁸ segundos en recorrer el espacio completo. La edad del universo ronda los 10¹⁷ segundos. La operación inversa se encuentra completamente fuera de alcance.

Qué ocurre con los ordenadores cuánticos

El algoritmo de Shor podría, en teoría, resolver este problema de forma eficiente. Para hacerlo con claves de 256 bits sería necesario disponer de cientos de cúbits lógicos con corrección de errores completa. Esto exige millones de cúbits físicos y circuitos profundos y extremadamente estables. La tecnología cuántica actual trabaja con cúbits ruidosos y sin la corrección de errores necesaria para ejecutar un ataque de este tipo. En estas condiciones los ordenadores cuánticos reales no suponen una amenaza para ECDSA ni para Bitcoin.

Una verdadera amenaza cuántica

Para que un ataque cuántico contra Bitcoin o RSA fuera realmente viable, no bastaría con un procesador de unas pocas decenas o incluso cientos de cúbits físicos. Sería necesario un tipo de máquina cuántica radicalmente más avanzada que las actuales. En concreto, un ataque práctico requeriría:

• Cúbits lógicos y corrección de errores completa. La criptografía moderna no cae con cúbits físicos: hace falta ejecutar el algoritmo de Shor de forma tolerante a fallos. Esto implica miles de cúbits lógicos, cada uno respaldado por miles de cúbits físicos mediante códigos de corrección de errores.
• Profundidad de circuito muy elevada. Shor, aplicado a claves reales de 2048 o 3072 bits (RSA) o a claves de 256 bits en curvas elípticas (Bitcoin), exige millones de puertas cuánticas consecutivas. Los dispositivos actuales apenas soportan unas decenas.
• Tasas de error ultrabajas. Incluso un pequeño error acumulado destruye el estado cuántico y hace fracasar la ejecución. Se necesitarían tasas de error por puerta y por qubit varios órdenes de magnitud mejores que las actuales.
• Quantum RAM (QRAM). Para manejar eficientemente estructuras de datos a la escala necesaria en ataques criptográficos. La QRAM no es estrictamente necesaria para ejecutar Shor, pero sería imprescindible para escalar muchos ataques criptográficos cuánticos más avanzados y hoy sigue siendo solo un concepto teórico.
• Estabilidad durante tiempos largos. Ejecutar Shor sobre claves reales demandaría minutos u horas de operación coherente, mientras que los sistemas actuales mantienen la coherencia durante milisegundos o microsegundos.

Solo la combinación de estos elementos permitiría, en la práctica, romper RSA o ECDSA. Y ninguno de ellos está disponible hoy. La distancia tecnológica entre los ordenadores cuánticos actuales y una máquina capaz de atacar criptografía real sigue siendo enorme.

Conclusión

El supuesto “ataque cuántico a Bitcoin en 320 segundos” no solo era falso, sino técnicamente imposible con el hardware cuántico disponible hoy. Tanto RSA como las curvas elípticas que utiliza Bitcoin se basan en problemas matemáticos cuya inversión sigue estando muy lejos del alcance de los ordenadores cuánticos actuales. El algoritmo de Shor demuestra que, en teoría, el futuro cuántico podrá romper ambos sistemas, pero ese escenario exige miles de cúbits lógicos y millones de cúbits físicos, una escala que ninguna plataforma cuántica moderna puede ofrecer.

Mientras tanto, Bitcoin continúa protegido por ECDSA sobre secp256k1, una estructura criptográfica altamente resistente y con niveles de seguridad equivalentes a claves RSA mucho más largas. La amenaza cuántica llegará si la tecnología consigue escalar de forma significativa, algo que hoy está muy lejos de estar resuelto. Será un proceso gradual que la comunidad criptográfica, las infraestructuras de Internet y las cadenas de bloques tendrán que afrontar mediante algoritmos postcuánticos estandarizados.

Referencias

Shor, P. W. (1994). Algorithms for quantum computation: Discrete logarithms and factoring. IEEE FOCS. https://doi.org/10.1109/SFCS.1994.365700

Nakamoto, S. (2008). Bitcoin: A Peer-to-Peer Electronic Cash System. https://bitcoin.org/bitcoin.pdf

Hankerson, D., Menezes, A., Vanstone, S. (2004). Guide to Elliptic Curve Cryptography. Springer. https://link.springer.com/book/10.1007/b97644

NIST (2022). Post-Quantum Cryptography Standardization Project. https://csrc.nist.gov/projects/post-quantum-cryptography

Bernstein, D. J., Lange, T. (2017). Post-quantum cryptography. Nature 549, 188–194. https://doi.org/10.1038/nature23461

Google Quantum AI (2019). Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510. https://www.nature.com/articles/s41586-019-1666-5

Google Quantum AI (2024). Información técnica del procesador Willow (105 cúbits). https://quantumai.google

IETF (2018). RFC 8446: The Transport Layer Security (TLS) Protocol Version 1.3. https://datatracker.ietf.org/doc/rfc8446/

Bernstein, D. J., Buchmann, J., Dahmen, E. (2009). Post-Quantum Cryptography. Springer. https://link.springer.com/book/10.1007/978-3-540-88702-7

Menezes, A., Van Oorschot, P., Vanstone, S. (1996). Handbook of Applied Cryptography. CRC Press. https://cacr.uwaterloo.ca/hac/